조합

2022-05-18 6 분 소요

조합(nCr)

조합이란 n 개의 숫자 중에서 r개의 숫자를 순서없이 뽑는 경우를 말한다.

[1, 2, 3] 의 조합 3C2 = (1, 2) (1, 3) (2, 3) 이다.

순서없이 뽑기때문에 (1, 2) 와 (2, 1)은 같다고 보고 둘중 하나만 선택된다.

특징

조합은 nCr 로 표현된다.

5C2 = 5 x 4 / 2 x 1 = 5C3 = 5 x 4 x 3 / 3 x 2 x 1 = 10

nC0 = nCn = 1

nCr = n-1Cr-1 + n-1Cr 로 나타낼 수 있다.

즉, 조합은 하나의 원소를 선택할 경우 + 하나의 원소를 선택하지 않을 경우 이 둘의 합이다.

[1,2,3] 중에서 2개를 뽑는 조합 » 3C2

3C2 = 2C1 + 2C2

1을 뽑는 경우 나머지 2개(2, 3) 중 1개 선택한다. » 2C1

1을 뽑지 않는 경우 나머지 2개(2, 3) 중 2개를 선택한다. » 2C2

조합의 경우의 수 구하기

nCr 결과를 알아내는 것이다.

3C2 = 2C1 + 2C2 = 2 + 1

2C2 = 2C0 = 1

2C1 = 1C1 + 1C0 = 1 + 1 = 2

즉, n == r 인 경우 or r == 0인 경우를 찾는것이다. (이때 nCr =1) 그 전까지 재귀 호출(원소 선택 + 원소 선택하지 않을 경우)

	//nCr
    public static int combination(int n, int r) {
        //nCn = 1, nC0 = 1
        if (n == r || r == 0) {
            return 1;
        } else {    //nCr = n-1Cr-1 + n-1Cr
            return combination(n - 1, r - 1) + combination(n - 1, r);
        }
    }

조합 쌍 구하기

arr: 조합을 뽑아낼 배열
r: 뽑을 개수
visited: 조합에서 뽑힌 원소인지 확인하기 위한 배열

배열 모두 돌며 완전 탐색

현재 인덱스가 선택된 경우, 현재 인덱스를 선택하지 않는 경우

r == 0 이면 r개를 모두 뽑은것

구현 방법으로는 백트래킹, 재귀 두가지 방법이 있다.

백트래킹으로 구현

start: 탐색 기준(index = start 인 경우부터 선택, 선택하지 않는 경우구함), start를 늘려가며 탐색하기에 start 이전 index는 다 확인이 끝났다.

start를 기준으로 index = start 인 경우부터 배열을 완전탐색하며 arr[index] 원소를 선택할 경우, 선택하지 않을 경우를 탐색한다.

arr[index] 원소를 선택할 경우는 index = start일때 다 찾아지고

선택하지 않을 경우는 index를 1씩 키워가며 확인하는 이후 과정에서 구해진다.

	//조합 묶음 구하기 : [1,2,3] >> (1,2) (1,3) (2,3)
    //백트래킹 방법
    //start 는 기준으로 start부터 쌍 확인, start 이전 내용은 다 체크한것으로 간주
    public static void comb1(int[] arr, boolean[] visited, int start, int n, int r) {
        if (r == 0) {
            print(arr, visited, n);
            return;
        } else {
            //순서대로 자신 뽑는 경우 확인, 뽑지 않는 경우는 현재 i 보다 큰 나머지 들에서 확인됨
            for (int i = start; i < n; i++) {
                visited[i] = true;
                comb1(arr, visited, i + 1, n, r - 1);
                visited[i] = false;
            }
        }
    }
    
    //조합 쌍 출력
    public static void print(int[] arr, boolean[] visited, int n) {
        for (int i = 0; i < n; i++) {
            if (visited[i] == true) {
                System.out.print(arr[i] + " ");
            }
        }
        System.out.println();
    }

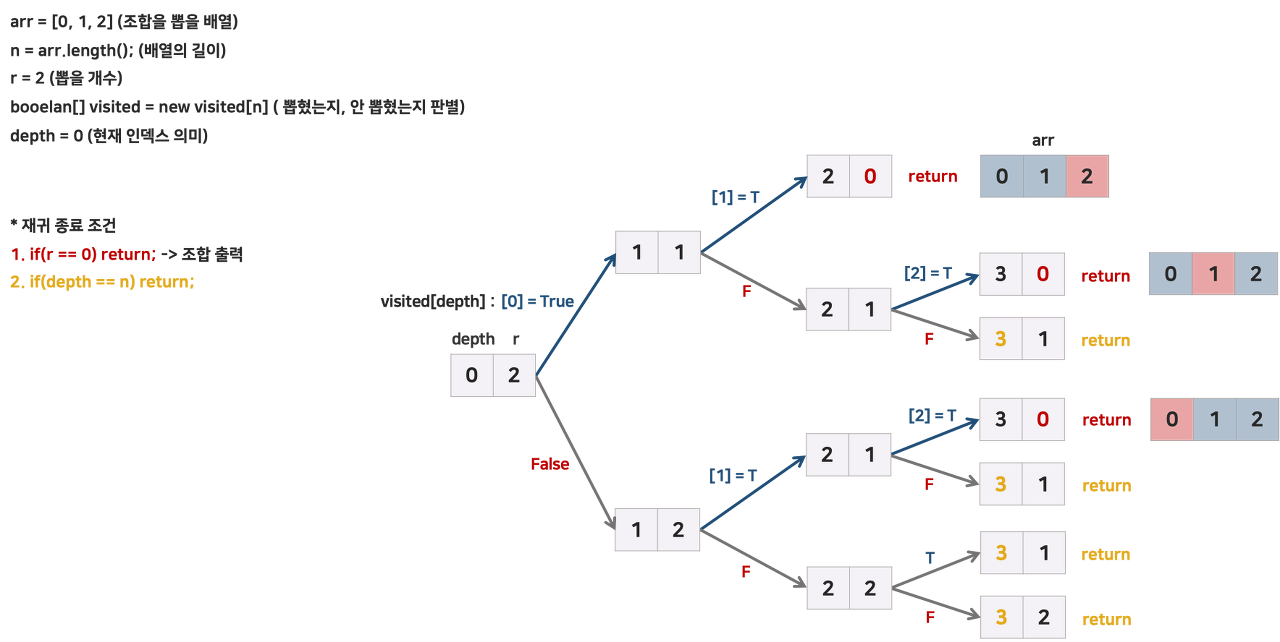
재귀로 구현

depth: 현재 인덱스, 0부터 시작한다.

n은 그대로 두고 depth 를 1씩 키워가면 n범위가 그만큼 줄어드는것

원소를 뽑은 경우, 뽑지 않은 경우를 모두 탐색해야 하고 이전에 본 값들은 더이상 대상이 아니라서 depth 를 1씩 증가시킨다.(앞에서 start 증가시켰던것 처럼)

r == 0은 뽑아야 하는 개수만큼 모두 뽑아서 조합이 완성되었으므로 재귀를 종료한다.

depth == n 인 경우는 r개 만큼 다 뽑지 못했지만 모든 인덱스를 다 봤기에 재귀를 종료한다.

comb1

	//조합 묶음 구하기 : [1,2,3] >> (1,2) (1,3) (2,3)
    //재귀
    public static void comb2(int[] arr, boolean[] visited, int depth, int n, int r) {
        //다 찾음
        if (r == 0) {
            print(arr, visited, n);
            return;
        }
        //못 찾았는데 끝남
        if (depth == n) {
            return;
        }
        else {
            //하나의 원소 선택한 경우 n-1Cr-1
            //n-1Cr-1에서 n-1은 depth + 1을 함으로 탐색 대상을 줄였다.
            visited[depth] = true;
            comb2(arr, visited, depth + 1, n, r - 1);

            //하나의 원소를 선택하지 않은 경우 n-1Cr
            //n-1Cr에서 n-1은 depth + 1을 함으로 탐색 대상을 줄였다.
            visited[depth] = false;
            comb2(arr, visited, depth + 1, n, r);
        }
    }
    
    //조합 쌍 출력
    public static void print(int[] arr, boolean[] visited, int n) {
        for (int i = 0; i < n; i++) {
            if (visited[i] == true) {
                System.out.print(arr[i] + " ");
            }
        }
        System.out.println();
    }

전체 코드

public class Combination {

    //nCr
    public static int combination(int n, int r) {
        //nCn = 1, nC0 = 1
        if (n == r || r == 0) {
            return 1;
        } else {    //nCr = n-1Cr-1 + n-1Cr
            return combination(n - 1, r - 1) + combination(n - 1, r);
        }
    }

    //조합 묶음 구하기 : [1,2,3] >> (1,2) (1,3) (2,3)
    //백트래킹 방법
    //start 는 기준으로 start부터 쌍 확인, start 이전 내용은 다 체크한것으로 간주
    public static void comb1(int[] arr, boolean[] visited, int start, int n, int r) {
        if (r == 0) {
            print(arr, visited, n);
            return;
        } else {
            //순서대로 자신 뽑는 경우 확인, 뽑지 않는 경우는 현재 i 보다 큰 나머지 들에서 확인됨
            for (int i = start; i < n; i++) {
                visited[i] = true;
                comb1(arr, visited, i + 1, n, r - 1);
                visited[i] = false;
            }
        }
    }

    //조합 묶음 구하기 : [1,2,3] >> (1,2) (1,3) (2,3)
    //재귀
    public static void comb2(int[] arr, boolean[] visited, int depth, int n, int r) {
        //다 찾음
        if (r == 0) {
            print(arr, visited, n);
            return;
        }
        //못 찾았는데 끝남
        if (depth == n) {
            return;
        }
        else {
            //하나의 원소 선택한 경우 n-1Cr-1
            //n-1Cr-1에서 n-1은 depth + 1을 함으로 탐색 대상을 줄였다.
            visited[depth] = true;
            comb2(arr, visited, depth + 1, n, r - 1);

            //하나의 원소를 선택하지 않은 경우 n-1Cr
            //n-1Cr에서 n-1은 depth + 1을 함으로 탐색 대상을 줄였다.
            visited[depth] = false;
            comb2(arr, visited, depth + 1, n, r);
        }
    }

    //조합 쌍 출력
    public static void print(int[] arr, boolean[] visited, int n) {
        for (int i = 0; i < n; i++) {
            if (visited[i] == true) {
                System.out.print(arr[i] + " ");
            }
        }
        System.out.println();
    }

    public static void main(String[] args) {
        System.out.println("-------- 0. 조합 경우의 수 ---------");
        System.out.println(combination(3, 2));
        System.out.println();

        //조합 만들 배열
        int[] arr = {1, 2, 3};
        //arr의 각 원소 기준으로 방문 여부 체크
        boolean[] visited = new boolean[arr.length];

        //nC1, nC2 ,,, nCn 각 쌍
        //백트래킹 이용해서 구현
        System.out.println("-------- 1. 백트래킹 ---------");
        for (int r = 1; r <= arr.length; r++) {
            System.out.print(arr.length + "개 중에 " + r + "개 뽑음");
            System.out.println();
            comb1(arr, visited, 0, arr.length, r);
            System.out.println();
        }

        //nC1, nC2 ,,, nCn 각 쌍
        //재귀 이용해서 구현
        System.out.println("\n---------- 2. 재귀 ----------");
        for (int r = 1; r <= arr.length; r++) {
            System.out.print(arr.length + "개 중에 " + r + "개 뽑음");
            System.out.println();
            comb2(arr, visited, 0, arr.length, r);
            System.out.println();
        }
    }
}

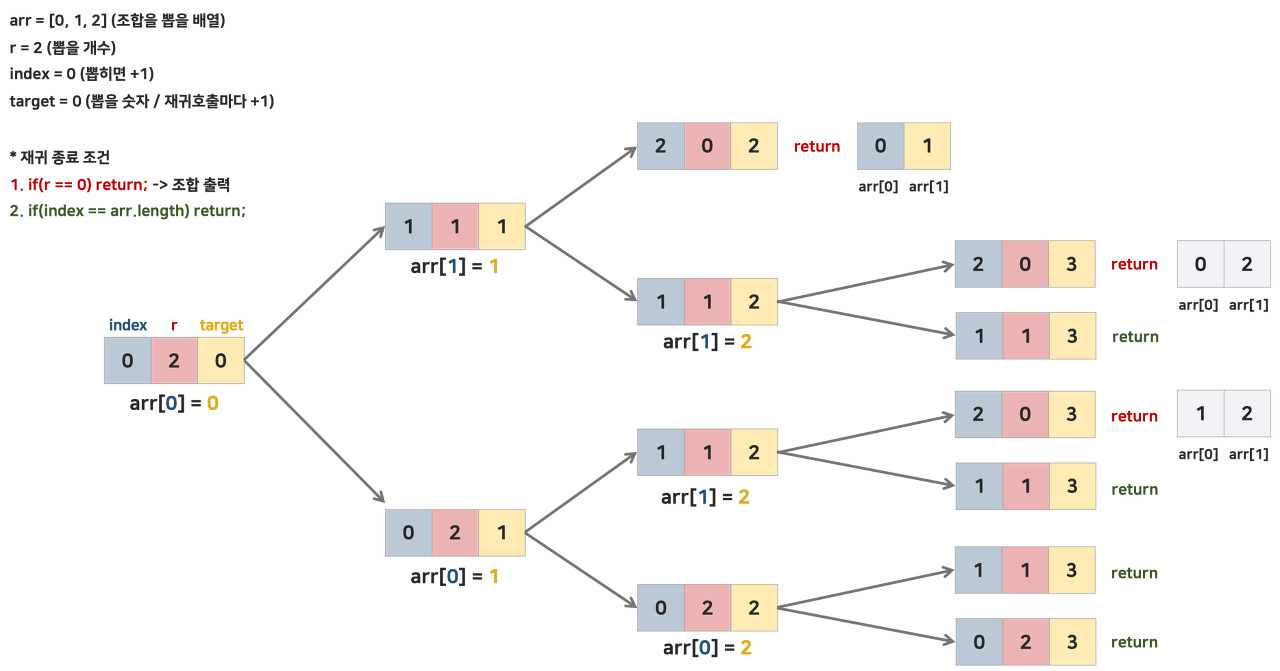
visited 배열 사용하지 않고 정수 변수 index로 구현

0 ~ n까지의 숫자 조합을 구하는 방법이다.

arr: 배열은 사이즈 n으로 0 ~ n 중 선택된것들이 채워진다. 조합의 쌍
index: 0부터 시작해서 arr의 현재 채울 대상을 나타내는 인덱스이다. target이 뽑히면 arr[index] = target으로 조합 쌍에 넣고 다음에 뽑힌 값은 arr의 index+1에 들어가야 하므로 현재 index 값을 1 증가 시킨다. (뽑히면 index + 1, r-1 / 안 뽑히면 index, r 그대로)
target 은 뽑을지 판단되는 대상으로 뽑으면 arr[index] 에 넣는다. 안뽑히면 넘어감, 때문에 target은 매 단계마다 항상 1씩 증가한다. target + 1은 nCr에서 n-1 -> n-2 -> ,,, -> 1까지 가는 역할을 한다.

종료 조건은 재귀를 이용한 구현과 같다.

comb2

	//visited 없이 index로 해결
    public static void comb3(int[] arr, int index, int n, int r, int target) {
        if (r == 0) {
            print3(arr, index);
        }
        else if (target == n) {
            return;
        }
        else{
            arr[index] = target;
            comb3(arr, index + 1, n, r - 1, target + 1);
            comb3(arr, index, n, r, target + 1);
        }
    }

    public static void print3(int[] arr, int length) {
        for (int i = 0; i < length; i++) {
            System.out.print(arr[i] + " ");
        }
        System.out.println();
    }

	public static void main(String[] args) {
    	int[] arr3 = new int[3];
        	//0 ~ n-1
	        System.out.println("---------- 3. visited 없이 index로 해결 ----------");
	        comb3(arr3, 0, 3, 2, 0);
	}

참고: https://minhamina.tistory.com/38?category=837168

###

Twitter Facebook LinkedIn

조합

조합(nCr)

특징

조합의 경우의 수 구하기

조합 쌍 구하기

백트래킹으로 구현

재귀로 구현

전체 코드

visited 배열 사용하지 않고 정수 변수 index로 구현

공유하기

댓글남기기

참고

git stash

전략 패턴(Strategy Pattern)

템플릿 메서드 패턴(Template Method Pattern)

잠금을 통한 동시성 해결하기